2010-2011

Vendredi 1^er juillet 2011 : Gábor Hetyei http://www.math.uncc.edu/~ghetyei/

Titre : Les jeux du type Bernoulli et un nouveau type de formules en combinatoire énumérative

Résumé : Nous introduisons un jeu de troncature à deux joueurs sur les paires de mots de même longueur, tel que le nombre des positions de longueur n où le deuxième joueur a une stratégie gagnante est (n+1)! fois la valeur absolue du n^ième nombre de Bernoulli de deuxième espèce. Une généralisation de ce jeu nous offre un modèle combinatoire pour les nombres de Bernoulli dégénérés introduits par Carlitz. Une application probabiliste réalise l'intégrale de n'importe quelle fonction sur un intervalle fini comme le gain attendu dans un jeu aléatoire infini.
Ce qui rend facile de compter les positions gagnantes dans nos exemples est le fait qu'à chaque tour la stratégie ne permet qu'un seul bon coup. Nous décrivons une classe de jeux avec cette propriété qui nous offre une nouvelle interprétation combinatoire de plusieurs formules. Dans une sous-classe des jeux de troncature sur les mots on peut décomposer les positions gagnantes en positions gagnantes élémentaires, d'une manière unique. Ainsi nous obtenons des nouvelles formules pour les nombres et polynômes de Bernoulli de deuxième espèce et nous retrouvons une variante de la décomposition des permutations indécomposables qui a été utilisée par King pour construire un code Gray pour les permutations indécomposables.

Vendredi 24 juin 2011 : Mireille Bousquet-Mélou

Titre : Le nombre d'intervalles dans les treillis de m-Tamari

Résumé : On considère l'ensemble T_n^m des chemins du plan issus de (0,0), formés de pas nord et est, finissant en (mn,n), et restant au dessus de la droite d'équation x=my. François Bergeron a décrit sur ces chemins un ordre, qui généralise l'ordre de Tamari (obtenu pour m=1). On verra que cet ordre donne une structure de treillis, pour tout m.
François a conjecturé une belle formule --- qui ressemble à un nombre de cartes, soit un coefficient binomial divisé par deux termes linéaires en n --- pour le nombre d'intervalles dans le treillis T_n^m. C'est cette formule qu'on démontre. Elle était connue depuis quelques années pour m=1, d'abord prouvée récursivement par Chapoton, puis par Bernardi et Bonichon via une bijection avec des triangulations. Pour m général, une approche bijective reste à inventer, et nous procédons récursivement.
Selon François B., ces mêmes nombres donnent la dimension d'un certain espace de polynômes --- mais c'est là une tout autre histoire, à coup sûr bien plus difficile.

Travail en commun avec Éric Fusy (LIX) et Louis-François Préville Ratelle (LACIM).

Vendredi 10 juin 2011 : Philippe Narbel

Titre : Shifts, échanges d'intervalles et arbres

Résumé : On présentera ici des relations entre les shifts (i.e. les langages fermés invariants par décalage), et les échanges d'intervalles, eux-mêmes liés à des représentations arborescentes de la combinatoire des mots de ces mêmes shifts.

Vendredi 27 mai 2011 : Adrien Boussicault

Titre : Arbres non ambigus servis avec leurs myriades d'arbres planaires

Résumé : Les arbres non ambigus sont des dessins particuliers d'arbres binaires sur le quadrillage. Ce sont des objets qui apparaissent naturellement dans les tableaux boisés. Dans cet exposé, nous utilisons les bijections classiques entre arbres binaires et arbres planaires pour
- engendrer les arbres non ambigus d'un arbre binaire donné ;
- compter les arbres non ambigus d'un arbre binaire donné ;
- réaliser une bijection simple entre polyominos parallélogrammes et arbre binaires.

Enfin, nous donnons une bijection entre les tableaux boisés et les arbres non ambigus escaliers.

Vendredi 20 mai 2011 : Sandrine Dasse-Hartaut

Titre : Introduction aux tableaux escaliers

Résumé : On présentera les tableaux escaliers (généralisation des tableaux de permutation, et en bijection avec les permutations doublement signées), et quelques pistes utilisées pour les comprendre, notamment la construction de ces tableaux par récurrence, qui a donné lieu à une étude des lois des paramètres des tableaux, ou la mise en bijection de sous-ensembles de ces tableaux avec des permutations.

Vendredi 13 mai 2011 : Adrien Boussicault

Titre : Tableaux boisés servis avec leur algorithme d'insertion

Résumé : Dans cet exposé nous présentons les tableaux boisés. Les tableaux boisés sont des objets en bijection simple avec les tableaux de permutation et les tableaux alternatifs. Nous introduisons ensuite un algorithme d'insertion élémentaire sur nos tableaux qui donne une preuve simple que les tableaux de taille n sont comptés par n!. Nous expliquons comment, à partir de cet algorithme, il est possible de construire un patron de bijections entre les tableaux boisés et les permutations. Nous utilisons ensuite ce patron pour faire apparaître
- des bijections directes entre tableaux boisés et permutations;
- de nombreuses statistiques;
- des formules d'énumération.

Enfin, nous montrons comment il est possible de modifier l'algorithme d'insertion pour étudier la combinatoire des :
- tableaux boisés symétriques ( type B )
- chemins de Dycks valués
- partitions gauches

Vendredi 6 mai 2011 : Valentin Féray

Titre : Inclusion/Exclusion cyclique

Résumé : Certaines formules pour les caractères du groupe symétrique s'expriment à l'aide de briques de base simples : des séries génératrices de fonctions sur des ensembles ordonnés. Dans cet exposé, nous regarderons les relations linéaires entre ces séries génératrices. Celles-ci peuvent être décrites à l'aide d'une opération combinatoire locale simple que nous appelons inclusion/exclusion cyclique.

Vendredi 29 avril 2011 : Eric Fusy

Titre : Algorithmes barycentriques pour le dessin de graphes dans le plan

Résumé : Nous proposons un survol de deux algorithmes de dessin bien connus pour dessiner un graphe dans le plan: celui de Tutte et celui de Schnyder. Tous deux utilisent un principe barycentrique de placement des sommets, cependant de manière tres différente. Si le temps le permet nous montrerons aussi d'autres algorithmes plus récents du type de celui de Schnyder.

Vendredi 15 avril 2011 : Frédéric Mazoit

Titre : Hypergraphes sur des surfaces: dualité et largeur arborescente

Résumé : Le dual d'un graphe planaire G est obtenu en plaçant un sommet par face de G et en ajoutant pour toute arête e de G une arête qui relie les centres des faces incidente à e. Cette notion classique s'étend sans problème aux plongements cellulaires sur des surfaces quelconques. Elle se généralise aussi aux hyper cartes qui sont des plongements d'hypergraphes sur des surfaces orientables.

Par ailleurs, les travaux de Bruno Courcelle ont montré que la largeur arborescente peut servir de mesure de "complexité" des graphes. Comme il semblerait curieux que la "complexité" d'un plongement et cette de son dual soit très différente, on s'attend à ce que la largeur arborescente d'un plongement et celle de son dual soit proche.

Dans cet exposé, montrerai comment définir une dualité pour les hypergraphes plongés dans des surfaces quelconques et comment j'ai utilisé cette extension pour obtenir un lien entre la largeur arborescente d'un plongement et celle de son dual.

Vendredi 8 avril 2011 : Philippe Gambette

Titre : Méthodes combinatoires de reconstruction de réseaux phylogénétiques .

Résumé : Les réseaux phylogénétiques généralisent le modèle de l'arbre pour décrire l'évolution, en permettant à des arêtes entre les branches de l'arbre d'exprimer des transferts de matériel génétique entre espèces coexistantes. De nombreuses approches combinatoires ont été conçues pour reconstruire ces réseaux à partir de données extraites de plusieurs arbres de gènes contradictoires. Elles se divisent en plusieurs catégories selon le type de données en entrées (triplets, quadruplets, clades ou bipartitions) et les restrictions de structure sur les réseaux reconstruits. Je présenterai deux approches combinatoires de reconstruction de réseaux phylogénétiques, à partir de clades ou de quadruplets, ainsi que des propriétés de structure des réseaux qu'elles reconstruisent. Je montrerai également des limites de de ces méthodes, et la façon de les prendre en compte, en particulier par des pré-traitements appropriés des données.

Vendredi 1er avril 2011 : Pierre-Loïc Méliot

Titre : Battages de cartes, partitions aléatoires et théorème central limite pour les caractères du groupe symétrique infini.

Résumé : À tout caractère irréductible du groupe symétrique infini, on associe des mesures de probabilité P_n et Q_n sur l'ensemble Y_n des partitions de l'entier n et sur l'ensemble S_n des permutations de taille n. La mesure Q_n peut être décrite par un algorithme de battages de cartes ; la mesure P_n est l'image de Q_n par l'algorithme de Robinson-Schensted, et elle correspond également à la décomposition du caractère initial dans la base des caractères irréductibles de S_n. On s'intéressera aux propriétés asymptotiques des mesures P_n, et on présentera une loi des grands nombres due à Kerov et Vershik, ainsi qu'un théorème central limite. S'il reste du temps, on évoquera aussi le lien conjectural entre les mesures Q_n, les mouvements browniens conditionnés à rester dans une chambre de Weyl et les valeurs propres de matrices hermitiennes browniennes.

Vendredi 25 mars 2011 : Alexandre Zvonkine

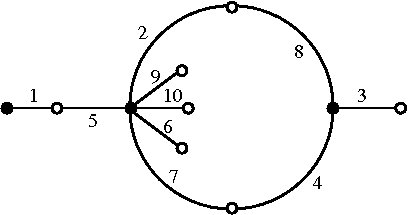
Titre : Sur le problème de moments pour les polynômes de Laurent

Résumé : L'exposé sera dédié à une étude approfondie du dessin suivant :

Vendredi 18 mars 2011 : Axel Bacher

Titre : Excursions discrètes de hauteur bornée

Résumé : Considérons les chemins de Dyck de hauteur bornée par k. La série comptant ces chemins est de la forme F_{k-1}/F_k, où les F_k sont les polynômes de Fibonacci. Nous verrons que ces polynômes se factorisent en deux termes, qui suivent la même récurrence linéaire que les F_k. Nous donnerons une explication combinatoire de ce fait.

Ces résultats persistent dans un cadre plus général, étudié par Banderier et Flajolet (2001), puis par Bousquet-Mélou (2008), où les chemins peuvent suivre des pas appartenant à un ensemble S fixé symétrique (par exemple -2,-1,+1,+2). Nous donnerons encore une interprétation combinatoire des polynômes impliqués et de leurs facteurs.

Vendredi 4 mars 2011 : Alice Jacquot

Titre : Reconnaissance et génération aléatoire de polyominos digitalement convexes

Résumé : Un polyomino digitalement convexe est l'ensemble des cellules intérieures d'une region convexe du plan. S. Brlek, J.-O. Lachaud, X. Provençal et C. Reutenauer ont donné un algorithme linéaire pour la reconnaissance de ces polyominos, basé sur une caractérisation combinatoire de leur mots de contour. Je présenterai cette caractérisation et je montrerai comment on peut en déduire un générateur aléatoire uniforme de polyominos digitalement convexes, faisant intervenir des générateurs de Boltzmann.

Vendredi 18 février 2011 : Philippe Duchon

Titre : Génération Boltzmannienne exacte avec oracles inexacts

Résumé : Le modèle de Boltzmann est une technique séduisante pour la génération aléatoires d'objets combinatoires, mais il a potentiellement le défaut de reposer sur un "oracle" chargé d'évaluer diverses séries génératrices en un même point. Une question naturelle est celle de l'influence, sur la qualité du résultat, de la précision numérique de l'oracle. On apportera à cette question des réponses plus ou moins satisfaisantes et intrigantes.

Vendredi 4 février 2011 : Philippe Duchon

Titre : Triangulations de l'hypercube, nombres eulériens, et simulation exacte de variables aléatoires

Résumé : On s'intéresse à la simulation exacte de la loi d'une somme de n variables aléatoires indépendantes, uniformes sur l'intervalle [0,1] (loi de Irvin-Hall). Plus précisément, peut-on obtenir une simulation exacte, sans opérations arithmétiques ?
La recherche d'une méthode "efficace" conduit, via les nombres eulériens et des résultats "bien connus depuis des siècles" sur le volume de "tranches" d'un hypercube, à un algorithme qui, en moyenne, utilise n log(n) + k bits aléatoires pour donner une précision de k bits sur la variable aléatoire simulée - ce qui bat asymptotiquement l'algorithme naïf à base d'additions en multiprécision.

Vendredi 21 janvier 2011 : Mireille Bousquet-Mélou

Titre : Sur la génération aléatoire des chemins auto-évitants

Résumé : Le point de départ de cet exposé est un algorithme proposé par D. Knuth en 1971 pour engendrer des chemins auto-évitants aléatoires traversant un carré de côté k du coin Sud-Ouest au coin Nord-Est. Aléatoires... mais pas uniformes. À partir des chemins aléatoires obtenus, on peut construire un estimateur du nombre de tels chemins. Knuth puis Diaconis se sont intéressés à la qualité de cet estimateur, plus précisément à sa variance, dont la détermination revient à compter (ouf !) ces chemins auto-évitants selon un certain poids.
On présentera quelques résultats autour de cette question, et bien sûr... d'autres questions.

Vendredi 14 janvier 2011 : Robert Cori

Titre : Preuve du théorème Riemann-Roch pour les graphes

Résumé : Suite de l'exposé du 17 décembre 2010 intitulé "Tas de sable sur un graphe et un théorème du style Riemann-Roch", après un rappel des notions nécessaires.

Vendredi 7 janvier 2011 : Valentin Féray

Titre : Approche algébrique et généralisation des formules d'équerre pour les arbres

Résumé : Une extension linéaire d'un ensemble ordonné P est un ordre total plus fin que P. Dans le cas où P est une forêt, Knuth a donné une très jolie formule en terme d'équerres pour dénombrer ces extensions linéaires. Des q-analogues de cette formule (prenant en compte l'indice majeur) ont été établis par Stanley, puis par Björner et Wachs.
L'objectif de cet exposé est de donner des interprétations algébriques de ces formules, en trouvant une présentation d'une certaine algèbre. Cette approche nous amène à considérer une classe de posets plus larges, appelés arbres décorés, pour lesquels on obtient des formules du même type.
Travail en commun avec Victor Reiner (University of Minnesota).

Vendredi 17 décembre 2010 : Robert Cori

Titre : Tas de sable sur un graphe et un théorème du style Riemann-Roch

Résumé : Dans le modèle du tas de sable on affecte à chaque sommet d'un graphe un entier positif ou nul censé représenter un nombre de grains situés sur le sommet en question. Une règle d'éboulement permet de faire passer des grains d'un sommet à ses voisins.
Deux généralisations du modèle avec l'affectation d'entiers pouvant être négatifs ont été considérées par différents auteurs. La première peut être interprétée par des particules et anti-particules qui se détruisent mutuellement lors d'un éboulement. La seconde comme des soldes de comptes en banque qui peuvent être redistribués aux voisins ou bien faire l'objet d'un versement collectif.
Il sera question dans cet exposé de résultats obtenus dans le cadre de ces deux modèles et en particulier d'un article de M. Baker et S. Norine dans Advances in Mathematics datant de 2007 et intitulé Riemann-Roch and Abel-Jacobi theory on a finite graph.

Vendredi 10 décembre 2010 : Mireille Bousquet-Mélou

Titre : Le nombre moyen d'inversions après n transpositions adjacentes

Résumé : On s'intéresse au nombre moyen d'inversions dans le produit de n transpositions adjacentes prises au hasard uniformément dans le groupe symétrique S_d, et au comportement asymptotique de ce nombre, lorsque d et n tendent vers l'infini à différents rythmes.

Vendredi 3 décembre 2010 : Mathilde Bouvel

Titre : Tri bulle et classes de permutations

Résumé : Dans cet exposé, on s'intéresse à l'opérateur B qui effectue une étape de tri bulle sur les permutations, et à l'action de cet opérateur et de son inverse sur les classes de permutations. Le résultat principal que je présenterai caractérise les permutations p telles que B^{-1}(Av(p)) est une classe de permutations, et le cas échéant décrit explicitement la base de cette classe.
Il s'agit d'un travail en collaboration avec Michael Albert, Mike Atkinson (Otago University), Anders Claesson (Reykjavik University) et Mark Dukes (University of Iceland).

Vendredi 26 novembre 2010 : François Bergeron http://bergeron.math.uqam.ca/Site/bergeron_uqam.html

Titre : Combinatoire de Catalan et des fonctions de stationnement

Résumé : Au cours des dernières années, des questions soulevées en théorie des invariants de groupes, concernant les propriétés des espaces coinvariants diagonaux, ont mené à une étude fine de la combinatoire des fonctions de stationnement (parking functions) et de paramètres sur celles-ci. Nous allons présenter certains de ces développements, ainsi que des extensions qui font intervenir l'ordre de Tamari et ses extensions aux cas des chemins de Dyck généralisés. L'emphase sera donc mise sur les problèmes combinatoires soulevés par cette étude.

Lundi 15 novembre 2010 : François Bergeron http://bergeron.math.uqam.ca/Site/bergeron_uqam.html

Titre : SL_k Pavages de ZxZ

Résumé : Il s'agit ici d'étudier les matrices bi-infinies d'entiers (ou de fractions rationnelles) qui satisfont la condition d'avoir tout mineur adjacent k x k égaux à 1. On dit de telles matrices que ce sont des SL_k Pavages de ZxZ. Après avoir exploré les propriétés générales de tels pavages (surtout dans le cas de rang minimal), nous allons décrire diverses façons d'en construire des familles d'exemples intéressants, entre autres via l'énumération (pondérées) de chemins. Des liens possibles avec les T-systèmes seront évoqués, ce qui montre l'intérêt de cette étude pour la construction de solutions particulières de l'équation de Hirota discrétisée.

Mercredi 10 novembre 2010 : Amarpreet Rattan http://www.ems.bbk.ac.uk/faculty/rattan

Titre : Lattice paths below a cyclically shifting boundary

Résumé : We count the number of lattice paths lying under a cyclically shifting piecewise linear boundary of varying slope. Our main result extends well known enumerative formulae concerning lattice paths, and its derivation involves a classical reflection argument. A refinement allows for the counting of paths with a specified number of corners. We also give various applications to recent results in the area of lattice path enumeration.
I will also present some very recent interesting extensions to this work.

Vendredi 5 novembre 2010 : Philippe Nadeau http://homepage.univie.ac.at/philippe.nadeau/

Titre : Sur certains polynômes énumérant les configurations de Fully Packed Loops

Résumé : Je parlerai de travaux récents en collaboration avec Tiago Fonseca sur l'énumération des Fully Packed Loops (FPLs). Le comptage des FPLs selon un certain diagramme de cordes associé donne lieu à de nombreux problèmes combinatoires, un des plus intéressants étant la correspondance de Razumov-Stroganov démontrée récemment par Cantini et Sportiello.
Dans cet exposé nous étudions les polynômes qui apparaissent lorsque l'on considère le nombre de FPLs associé à diagramme possédant un nombre croissant de "cordes imbriquées". Nous formulons notamment plusieurs conjectures sur les coefficients et les valeurs prises par ces polynômes, conjectures qui étayent l'existence d'un surprenant phénomène de "réciprocité combinatoire".

Vendredi 22 octobre 2010 : Adrien Boussicault

Titre : Les arbres ensoleillés

Résumé : Dans cet exposé, nous présenterons deux nouveaux objets : les arbres non ambigus et les arbres ensoleillés. Nous ferons ensuite le lien entre ces objets et les polyominos parallélogrammes d'une part et les tableaux de permutations d'autre part.
Ce travail est réalisé en collaboration avec Jean-Christophe Aval.

Vendredi 15 octobre 2010 : Yao-ban Chan (ARC Centre of Excellence for Mathematics and Statistics of Complex Systems (MASCOS))

Titre : Series expansions via the corner transfer matrix renormalization group method

Résumé : The corner transfer matrix renormalization group method is a powerful algorithm for evaluating physical quantities in statistical mechanical models. It was developed by Nishino and Okunishi in 1996, and originates from Baxter's corner transfer matrix equations and method, which were developed in 1978. The method has been applied to numerous models since its development to great success, but as far as we know has not been used to calculate series expansions (which Baxter did with his original method). In this talk, we discuss the CTM equations and method, the CTMRG method, and our work on this method which has enabled us to calculate series expansions from it.

Vendredi 8 octobre 2010 : Mireille Bousquet-Mélou

Titre : Chemins auto-évitants sur le réseau hexagonal d'après Duminil-Copin et Smirnov

Résumé : Les deux messieurs sus-nommés ont publié cet été une preuve (élémentaire !) d'une vieille conjecture (1982) sur le nombre c(n) de chemins auto-évitants de longueur n qu'on peut tracer sur le réseau hexagonal. Cette ex-conjecture décrit la croissance asymptotique de c(n) : c(n) ^ (1/n) converge vers sqrt(2+sqrt(2)). On présentera leur preuve.

Vendredi 1er octobre 2010 : matinée dédiée à Michel Marcus

Orateur : Valentin Féray

Titre : Énumération de cartes et calcul de caractères

Résumé : L'objectif de cet exposé est de présenter et de discuter les liens entre énumération de cartes (orientables) et caractères du groupe symétrique. Ces liens vont dans les deux directions : formule d'énumération utilisant des caractères et formules pour les caractères utilisant des cartes.
Si le temps le permet, je présenterai aussi les analogues de ces formules pour les cartes sur des surfaces localement orientables.

~~~~~

Orateur : Yves Métivier

Titre : Quelques résultats récents en algorithmique distribuée au LaBRI

Résumé : Cet exposé présentera des résultats obtenus récemment au LaBRI et se situant dans le prolongement du travail qui a été initié au département informatique de l'IUT. Plus précisément, il sera question des calculs locaux dans les graphes et du problème de l'élection ; puis d'algorithmes distribués probabilistes pour résoudre des problèmes dans les graphes comme le calcul d'un ensemble indépendant maximal, le coloriage ou bien le calcul d'une forêt couvrante.

~~~~~

Orateur : Gilles Schaeffer http://www.lix.polytechnique.fr/~schaeffe/

Titre : Bijections et cartes de genre supérieur

Résumé : Le plongement propre d'un graphe dans une surface orientable se décrit par une carte combinatoire. L'étude de ces cartes, et en particulier leur énumération, occupe des chercheurs depuis les travaux de l'illustre William T. Tutte, il y a près d'un demi-siècle... Pourquoi un tel acharnement ? Cette histoire durera-t-elle encore longtemps ? Michel pourra-t-il un jour vraiment prendre sa retraite ?
La partie technique de l'exposé portera sur une célèbre bijection de Cori et Vauquelin, et notamment sur l'opération d'éclatement de sommets qu'ils utilisent pour transformer petit à petit une carte en arbre bien étiqueté.
Cette opération peut s'interpréter sur les quadrangulations en terme de la règle des ronds points de Miermont. Dans sa thèse Michel Marcus indique le point clef qui lui a permis de généraliser la bijection de Cori-Vauquelin aux cartes de genre supérieur : il s'agit essentiellement de tourner toujours dans le même sens autour des ronds points, alors que ses illustres prédécesseurs prenaient les ronds points à l'anglaise une fois sur deux...

Vendredi 24 septembre 2010 : Bétréma

Titre : La preuve de la conjecture de Razumov et Stroganov par Cantini et Sportiello (1/2 et 2/2)

Transparents 1/4 Transparents 2/4 Transparents 3/4 Transparents 4/4

Vendredi 17 septembre 2010 : Pierre Nicodème http://www.lix.polytechnique.fr/Labo/Pierre.Nicodeme/

Titre : Bounded discrete walks (travail en commun avec Cyril Banderier)

Résumé : We consider the enumeration and asymptotics of directed lattice paths of bounded height (walks below one wall, or between two walls), for any finite set of jumps. We give the generating functions of bridges of a given height. Our formulae lead to fast algorithms for computing the n-th Taylor coefficients of the corresponding generating functions. For a large class of walks, we give the discrete distribution of the height of bridges, and show the convergence to a Rayleigh limit law. For the family of walks consisting of a -1 jump and many positive jumps, we give more precise bounds for the speed of convergence. This leads to a heuristic application to bioinformatics that has a high speed-up relative to previous work.

Vendredi 10 septembre 2010 : Guillaume Chapuy http://www.lix.polytechnique.fr/~chapuy/

Titre : Cartes à une face non-orientables

Résumé : En recollant bord à bord les arêtes d'un 2n-gone, on fabrique une surface topologique sur laquelle la trace du recollement forme le dessin d'un graphe à n arêtes. Ces objets, appelés cartes à une face, sont bien compris dans le cas orientable, grâce à des bijections apparues ces dernières années (par "orientable", j'entends que la surface obtenue est orientable, par exemple une sphère, ou un tore).
Le cas non-orientable pose des problèmes nouveaux, et c'est ce dont je parlerai. Je présenterai un résultat récent obtenu avec Olivier Bernardi (MIT), pour certaines cartes à une face non-orientables. On comptera exactement les cartes (pré)cubiques, et asymptotiquement toutes les cartes à une face (à surface fixée). Bien qu'inspirée de techniques "orientables", notre approche introduit une nouveauté importante : une involution qui, en un certain sens, "moyenne" les effets de la non-orientabilité. Il semblerait que les résultats énumératifs soient nouveaux.

Combinatoire et interactions

Equipe du département Combinatoire et Algorithmique

du LaBRI